I'm a big fan of the late Toby Hemenway's book, Gaia's Garden: A Guide to Home-Scale Permaculture. I own both editions, and for many years I used it as the curriculum for the intro permaculture courses I taught. In my opinion it's a classic right up there with Mollison's big black book. But since the publication of the 2nd edition in 2009, newer, better books on the subject have been published, and Hemenway publicly retracted some of the content of the book for being unsubstantiated, namely its recommendations of "dynamic accumulator" plants. When I met him in 2014, he brushed aside my praise for Gaia's Garden in favor of The Permaculture City, which was then nearing publication.
For a few months now I've been puzzling over some of his other recommendations in the book, of circular keyhole beds and in particular their arrangement into a "mandala" shape. I have come to the conclusion that these recommendations were also unsubstantiated, and I would bet that where they have been put into practice the results have not lived up to the hype. Unfortunately Hemenway passed away before I got this article written, so we will never know his opinion on the topic, but I'd be interested to hear what others have to say.
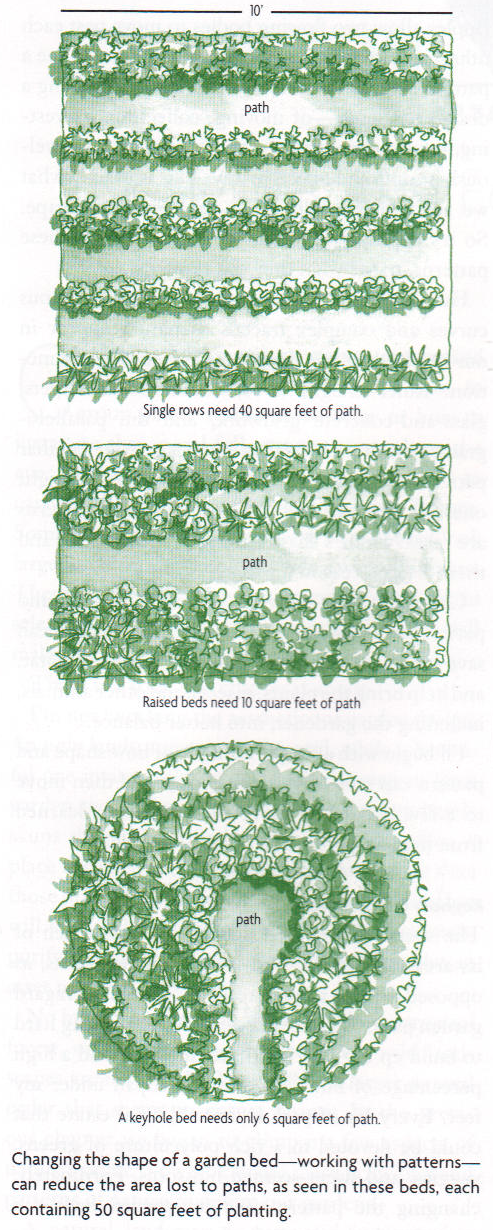 In the second edition of Gaia's Garden, where the ideas are more developed, Hemenway's argument for circular keyhole beds begins on page 38 with the three designs shown at left. From the width of the first garden and the square footage of path, we can deduce that the paths shown are 1 foot (1') wide. Note also that he is not counting any paths that may be on the perimeters of the gardens: only the interior paths are counted toward the square footage. I mention these assumptions because I'm going to carry them into my calculations on the other designs.
In the second edition of Gaia's Garden, where the ideas are more developed, Hemenway's argument for circular keyhole beds begins on page 38 with the three designs shown at left. From the width of the first garden and the square footage of path, we can deduce that the paths shown are 1 foot (1') wide. Note also that he is not counting any paths that may be on the perimeters of the gardens: only the interior paths are counted toward the square footage. I mention these assumptions because I'm going to carry them into my calculations on the other designs.
In the second design, he has reduced the amount of path by 75% by making the beds 2.5' wide instead of 1. So far so good; most adults can reach 2' from a squatting position, so 80% of the planted area is still reachable from the path in this design. It's a great improvement so far.
However, in the third design, the assumptions of the previous two go out the window. Hemenway explains in the accompanying text (p.38):
If we bend that rectangular raised bed into a circle—or, more accurately, a horseshoe shape—even more path will disappear. By a simple trick of topology, the path shrinks to a tiny keyhole shape, which gives this space-saving garden layout its name: keyhole bed.
Here's what happens. If we wrap a typical 4-by-15-foot raised bed into a U shape with a small central opening for a path, we cut the path down from about 22 square feet (figuring an 18-inch-wide path down one side of the raised bed) to 6 square feet. Less than a quarter of the ground is surrendered to paths. I won't torture you with the math that would prove this to the skeptical—as any publisher knows, each successive equation in a text puts half the remaining readers to flight.
Count me among the skeptical, then, because a couple of things about this explanation don't add up:
- In the previous two designs, the bed was not 4' by 15' (which would be 60 square feet, not 50), nor was the path 18" wide. He's not describing the "raised beds" shown in the second diagram, but an altogether different bed that is not pictured.
- If the circular bed in the diagram has 50 square feet (hereafter abbreviated sf) of planted area and 6sf of path, then the circle is 56sf, which means the radius is √(56/π) or 4.2'. (The only tortuous, frightening equation necessary here is A=π•r2, solved for r.)
- If the 6sf path is 18" (1.5') wide (for comparison with the rectangular raised bed he just described), then it is only 4' long and does not even reach into the center of the circle.
- If the path is a foot wide with a wider turn-around at the end (as shown in the diagram, and described in a sidebar on p.40), then the bed is still 4' wide from the path to the outer edge, putting 36% of the planted area out of reach of the path.
- To say that 6 is "less than a quarter" of 56 (or 60!) is a profound understatement. Why would he say less than a quarter when he means less than an eighth?
In the sidebar on page 40-41, Hemenway explains about the unreachable area:
In a keyhole bed, the plantable zone is about as wide as in a standard raised bed: 3 to 5 feet across. […] At the back of the bed, install long-term crops and those that are harvested only once. […] These back-row plants might be a bit out of reach if the bed is more than 3 feet deep; […] To harvest these plants, step onto the bed (gasp!) and pluck.
OK, so that means the circular keyhole design is not intended to put all the plants within reach of the path, or to put it a different way, part of the planted area is intended to be stepped on occasionally but is not being counted toward the square footage of path. But that means it's not a fair comparison to the other two designs above it! For a fair comparison, all we need do is shorten the path in the second design from 10' long to 8'. That brings the plantable area up to 52sf while keeping 77% of it (8•2•2+2+22π/2 = 40.3sf) within a 2' reach of the path, compared to at most 65% (32.3sf) of the circular design. The keyhole shape is great, but the rectangular design outperforms the circular one in both plantable area and reachable area!
Why does it matter? Because a generation of permaculturalists have read this book and implemented circular keyhole beds without verifying Hemenway's assertions of their mathematical superiority. A Google image search reveals that in most cases, the circular beds have been built free-standing, with a path all the way around the outside to allow access to those plants in the back! Assuming a 4.2' bed radius, this outer path is at least 29sf, for a total path area nearly 6 times more than the 6sf promised. This is a sub-optimal result, if not totally counterproductive.
In my own experience of implementing Hemenway's assertions, I have found that 1' wide paths are too narrow for comfort, and plants that are out of reach don't get adequate attention, and that stepping in the planted area to tend the farther plants is more disruptive to the garden than he implies. I find that I prefer to use wider paths and put as much of the garden within reach of the paths as possible.
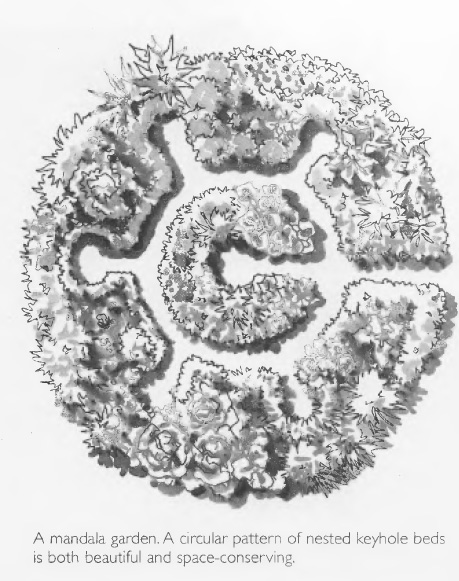 Hemenway goes on to propose a "mandala" garden design in which a central keyhole bed is surrounded by a ring of additional keyholes. It is notable that no dimensions are given either in Hemenway's design pictured at right (from p.39) or in any of the other published designs I can find. I'm going to assume that the central keyhole is the same 4.2' radius as before, with the surrounding path providing access to those hard-to-reach outer plants. I'm also going to assume that the outer keyholes have 6' paths. This makes the radius of the whole design 13.6' and the total area (including paths) 581sf.
Hemenway goes on to propose a "mandala" garden design in which a central keyhole bed is surrounded by a ring of additional keyholes. It is notable that no dimensions are given either in Hemenway's design pictured at right (from p.39) or in any of the other published designs I can find. I'm going to assume that the central keyhole is the same 4.2' radius as before, with the surrounding path providing access to those hard-to-reach outer plants. I'm also going to assume that the outer keyholes have 6' paths. This makes the radius of the whole design 13.6' and the total area (including paths) 581sf.
To calculate the area of paths and plantings within reach of the paths, I drew the design to scale (below -- click for full size). In the first (left) version, with six keyholes (including the one in the center) to match the published design, only 55% of the area is reachable from the paths. In the description on p.41, Hemenway says there may be up to 8 keyholes in the outer ring, for a total of 9 as shown in the second (center) version, bringing the reachable area up to 66%.
About this unreachable space, Hemenway explains (p.41) that it can be planted with beneficial insect attractants, nitrogen fixers, shrubs and trees, etc. But isn't that what's surrounding the circular mandala? After all, we're not counting the circumference of the garden as path... if we did, that would add a jaw-dropping 89sf of path, more than doubling what's shown in the design. So in my opinion, there's plenty of room for unreachable plants outside of the mandala. (Looking at Google images, it looks like as often as not, the mandalas have in fact been built free-standing with a path surrounding them.)
Hemenway concludes (p.41) that "Few designs can fit more growing space into less area" than his spoked mandala shape. But, assuming the same 13.6' radius and the same accessibility from only one spot on the circumference, I was able to put 72% of the total area within reach of paths (the third design, on the right), a 30% increase in reachable area with only a 9% decrease in total plantable area. One could argue that my design is not as aesthetically pleasing as the mandala shape. That may be, but it is in keeping with the biological pattern of leaf venation, which is appropriate to the flow of traffic in and out of the single garden entrance.
More generally, here is my preferred algorithm for optimizing keyhole paths in any shape of garden. It comes in handy for doodling during lectures!
- Identify which parts of the garden are already within reach. If the garden is already surrounded by path, this puts a 2' wide border within reach before you begin.
- Identify the least accessible point in the garden.
- Make a path from the nearest edge (or existing path), through this least-accessible point, continuing straight until the new path is within reach of the edge (or the area that's already reachable).
- Repeat steps 2 and 3 as long as each additional square foot of path makes more than one additional square foot of garden accessible.
When there is only one point of access, as in the mandala, this algorithm results in a branching shape reminiscent of leaf venation. When the entire perimeter of the garden is surrounded by path, it results in a sinuous shape reminiscent of the convolutions of the brain. In both cases, I believe these patterns are consistent with nature's solutions to similar problems, whereas the spoked mandala pattern is not.
To sum up, I am very much in debt to Toby Hemenway for his excellent books, and I was deeply honored to make his acquaintance and learn from him in person. However, I think the circular keyhole and mandala designs are conceptually flawed and should not be perpetuated. I'm working now on my own proposal for an ideal garden design which will be the subject of a future article. Thank you for reading!
- Log in to post comments





