 In my previous article, Rethinking keyhole beds and mandala gardens, I demonstrated that the circular horseshoe shape celebrated in permaculture as being mathematically and ergonomically optimal is in fact less optimal than a rectangular keyhole shape: it has less total growing space and less reachable space for a given amount of path. But what is the optimal arrangement of rectangular keyhole shapes? I've come to the conclusion that there is an optimal arrangement, and that it is a sinuous (winding) shape. This is mostly an academic point when planting directly in the ground, but it becomes a matter of economics when building raised beds.
In my previous article, Rethinking keyhole beds and mandala gardens, I demonstrated that the circular horseshoe shape celebrated in permaculture as being mathematically and ergonomically optimal is in fact less optimal than a rectangular keyhole shape: it has less total growing space and less reachable space for a given amount of path. But what is the optimal arrangement of rectangular keyhole shapes? I've come to the conclusion that there is an optimal arrangement, and that it is a sinuous (winding) shape. This is mostly an academic point when planting directly in the ground, but it becomes a matter of economics when building raised beds.
I make most of my garden beds directly in the soil, but there are a variety of reasons one might want to make raised beds. For example:
- The soil might be contaminated or full of persistent weeds.
- The soil might be inappropriate for the desired plants (too wet, too heavy, too sandy, too acid or alkaline).
- The gardener might not be able to bend down to ground level.
- The landscape might need texture to slow water erosion or create microclimates.
The traditional raised bed in the US is a rectangle 4 feet by 8 feet, since an average adult can reach two feet (2') in from the edge, and since dimensional lumber is typically sold in convenient 8' lengths (along with 6' and 10' options), allowing for inexpensive materials and a minimum of waste. However, anyone who has taken an intro to permaculture class or read a book on the subject knows that a keyhole shaped bed is theoretically more efficient than a rectangle, allowing the same amount of garden to be reached with less path than a rectangular design. A quick Google image search for "keyhole garden" turns up dozens of examples, but I can't help noticing that A) about half of them appear to be too small to benefit from the efficiency of the keyhole shape (since a 10' diameter is necessary to allow 2' reach on either side of a 2' path plus another 2' reach in from the outside); B) most of them are raised beds, necessitating both the exterior and interior perimeter to be constructed, and C) none of them are built with dimensional lumber because of the curved shape which Toby Hemenway and others claimed was more efficient than a rectangular one (and which I have since proved to be less efficient).
In the previous article, we considered two benchmarks (as percentages): plantable space divided by total space, and reachable space (within 2' of a path) divided by total space. Since we're now talking about raised beds, where the growing space cannot be easily stepped in and the perimeter of the beds must be constructed, the crucial benchmark is reachable area divided by perimeter. I'm going to talk about this ratio in units of square feet per foot (sf/ft) because I'm in the US, but the same ratios can be interpreted as square meters per meter (m2/m), keeping in mind that the average adult can only reach 0.6m (2') from a crouching position. If the beds are built up to waist high (so that the gardener need not squat down), an average adult can reach closer to 2.5' (0.75m).
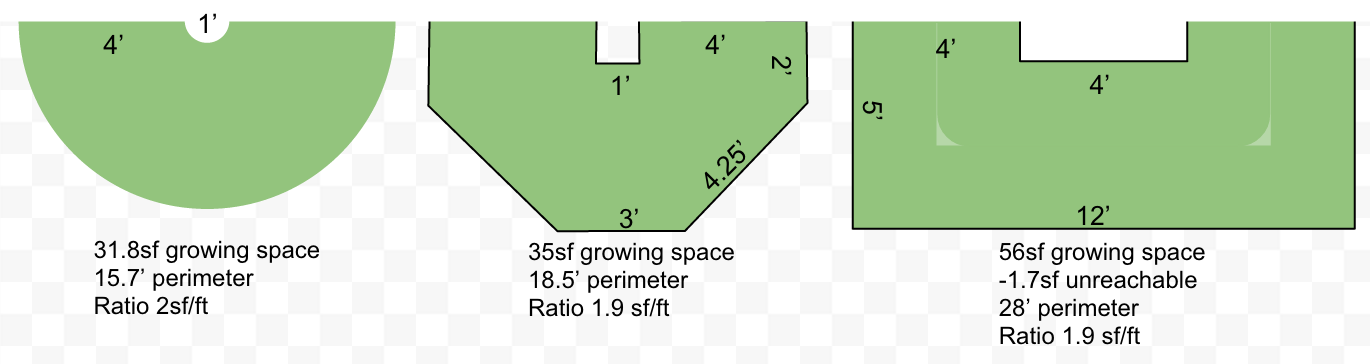
The theoretical maximum such ratio is at the end of a 1-foot-wide path (above left), where a 1 foot keyhole is surrounded by a 2' reach in a 180˚ semicircle, yielding a ratio of 6π/.5π = 12 sf/ft if you don't count the outside perimeter. However, we do need to count the outside perimeter as well, so that brings the ratio to 10π/5π or 2 sf/ft. What's interesting about using this benchmark instead of growing space / total space is that we no longer have to use those narrow 1' paths that Hemenway espoused. In fact, widening the path end reduces the impact of the pesky unreachable corners in a rectangular design, allowing us to use that cheap dimensional lumber and all right angles (above right).
 To understand why widening the paths doesn't hurt the ratio, let's consider another theoretical maximum. The second design in Hemenway's case for keyhole beds (shown at left) had a path surrounded on either side by "raised beds," though he didn't count the outer edges of the beds, only the inner ones along the path. Every linear foot of path (regardless of its width) thus has 2' of edge, giving access to 4sf of growing space, for a ratio of 2sf/ft regardless of how long the beds are.
To understand why widening the paths doesn't hurt the ratio, let's consider another theoretical maximum. The second design in Hemenway's case for keyhole beds (shown at left) had a path surrounded on either side by "raised beds," though he didn't count the outer edges of the beds, only the inner ones along the path. Every linear foot of path (regardless of its width) thus has 2' of edge, giving access to 4sf of growing space, for a ratio of 2sf/ft regardless of how long the beds are.
But again, we do have to consider the outside edges and ends, not just the inside edge. If we return to the traditional, 4x8' rectangular raised bed surrounded by path and apply this sf/ft benchmark, we quickly find that the best way to improve it is to extend it lengthwise. At 8' long, it has a ratio of 4•8/(8+16) = 1.3sf/ft, but at 16' long that goes up to 4•16/(8+32) = 1.6sf/ft, and if we built one 60' long, its ratio would be 4•60/(8+120) = 1.9. That's approaching the 2sf/ft economy of the beds with no outer perimeter, even though it's fully contained on all sides! (That is, the effect of enclosing the ends with lumber is reduced by putting more middle between the ends.)
 Of course, a 60' long garden would be very difficult to navigate, so we need to make it more compact by bending it around corners. Fortunately, each right-angle corner you put in the bed adds nothing to the perimeter and loses you only 4-π = 0.86sf of reachable space. The obvious conclusion would be that you want to minimize the number of corners. If you have a choice between making 3 short keyhole paths (6 corners) or one long one (2 corners), as shown at right, the long path with fewer corners will have more reachable space and so be very slightly more economical. However, the inconvenience of long keyholes may not justify the extra 3.5 sf of reachable space.
Of course, a 60' long garden would be very difficult to navigate, so we need to make it more compact by bending it around corners. Fortunately, each right-angle corner you put in the bed adds nothing to the perimeter and loses you only 4-π = 0.86sf of reachable space. The obvious conclusion would be that you want to minimize the number of corners. If you have a choice between making 3 short keyhole paths (6 corners) or one long one (2 corners), as shown at right, the long path with fewer corners will have more reachable space and so be very slightly more economical. However, the inconvenience of long keyholes may not justify the extra 3.5 sf of reachable space.
In fact, convenience and not economy should really be the deciding factor in determining which way to point the keyholes: they should go on the side(s) you're likely to approach the garden from. Point the paths toward zone 0 of your permaculture design! That makes the most area accessible without walking the long way around the garden.
The reason I describe these designs as "sinuous" is that as long as they don't branch, you can water the whole garden with a single soaker hose, which is important because raised beds tend to dry out more rapidly than beds in the ground. If the 3-keyhole design shown above had all three keyholes pointed up/north instead of one pointing down/south, it would have the same amount of reachable space, but it would be harder to water with a soaker hose.
The next question then becomes, how wide to make the paths? I propose making them 4' wide to match the width of the beds. The reason (besides ease of access) is that then the entire raised bed, no matter how many corners it turns, consists entirely of 4' squares, which means you can build a 4'x4' chicken coop (or rabbit hutch) to stand at any point along the bed (or in the path, for that matter), and build a chicken/rabbit run out of 4' panels that latch to the walls of the bed for security. When it's time to move this livestock tractor, just lift and slide it along the rails to the next position. [Note: this does not work. A subsequent article explains why and gives a better solution.]
What about changes in elevation? We've all seen raised beds built on a slope, such that one side is lower than the other and the topsoil washes out during a rain. Avoid that by building the bed along a contour line, as you would a swale. In fact, the beds can be the berm parts of the swales, with the (heavily mulched) paths serving as the ditches. To retain the benefit of the 4' square grid described above, make the sides of each 4x4' square level, and change elevation only at the corner posts.
Have I implemented these designs? Not yet, but I hope to do so soon! In the meantime, I'd love to hear your feedback. Please leave a comment below or email me through the contact form.
- Log in to post comments




